Figure 1 : Équation dynamique de la plate-forme. Inventaire des forces et des accélérations

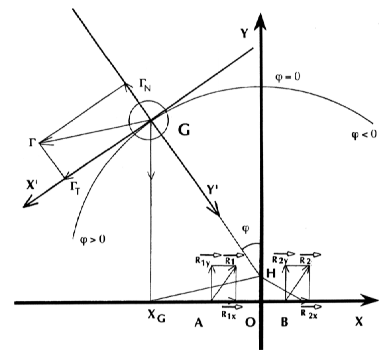
    1) Le système est indéformable.

    2) Le poids du sujet est positif, le référentiel lié au sujet subit donc par rapport au référentiel absolu une rotation de + (p+F) autour de G.

    3) OH = h      HG = L

        OA = a          M : Masse totale du sujet

        OB = b          XG = - Lsin F,     abscisse de G dans XOY.

    4) Les moments sont comptés positifs s'ils tendent à redresser l'axe du corps, négatifs dans le cas contraire.

    5) Le sujet est supposé en situation de chute avant :

       dF/dt = F ' > 0

       dF/dt2 = F " > 0

1) Equation des forces.

    Ce qui entraîne:

Rapportée au référentiel XOY cette équation permet d'écrire:

R1y + R2y - Mg = Mgy     (1)

R1x + R2x = Mgx             (2)

2) Equation des moments par rapport à H.

C'est à dire :

 

Compte-tenu des hypothèses 4 & 5 du §2:

aR1y - bR2y - h(R1x + R2x) - MgLsinF = -J.F"      (3)

3) Valeur de J.

    Le système en rotation autour de H équivaut à un pendule renversé de longueur L et de masse M, son moment d'inertie est égal à :

J=ML2

d'où:

- JF" = - ML2F"

De (1) on tire:

    R1y + R2y = Mg + Mgy (4)

de (2) et (3) il vient :

    aR1y - bR2y = MgLsinF - ML2F" + Mhgx  (5)

    G se décompose en GT et GN, accélérations tangentielle et normale, sur le système de référence X'GY'. gx  et gy se déduisent de GT et GN par un changement d'axes de coordonnées correspondant à une rotation du repère X'GY' de -(F+p) suivie d'une translation suivant l'axe OG du repère XOY de manière à superposer G et O. Dans ce cas la matrice de transformation est de la forme :

On a donc :

Dans le repère lié à G, G a pour coordonnées: GT, GN

Or -GN = -LF'2

et GT = LF"

d'où:

d'où :

gx = - L(F"cosF - F'2sinF)

gy  = - L(F"sinF + F'2cosF)

En reportant gx dans (5) il vient :

    aR1y - bR2y = MgLsinF - ML2F" + Mhgx - MhL(F"cosF - F'2sinF)

en multipliant droite et gauche par -1:

    bR2y - aR1y = MhL(F"cosF - F'2sinF)+ ML2F" - MgLsinF (6)

En reportant gy dans (4) il vient :

    R1y + R2y = Mg - ML(F"sinF + F'2cosF) (7)

Posons:

    X1 = (bR2y - aR1y) / (R1y + R2y)

En se reportant à (6) et (7) il vient :

d'où en simplifiant par M

    Sachant par ailleurs que XG = -LsinF , et en posant e = X1 - XG , il vient après réduction au même dénominateur:

soit :

(8)

    La relation (8) représente l'erreur absolue commise sur la détermination de la projection du centre de gravité sur le plan du polygone de sustentation. A noter que si F(t) = Cte on a F'(t) = F"(t) = e , ce qui prouve que cette erreur n'apparaît qu'en régime dynamique.

    Afin d'être plus général nous allons nous intéresser à présent à l'erreur relative e, définie par :

e = (X1 - XG ) / D

    avec D : valeur crête à crête du déplacement.

1 ) Définitions et conventions

Dans ce qui suit nous considérerons F sous la forme:

F (t) = F0 + F1 sin wt     (10)

F' (t) = F1 w cos wt        (11)

F'2 (t) = F12 w2 cos2wt  (12)

F"(t) = - F1 w2sinwt    (13)

2 ) Valeur des différents paramètres

    Le sujet étant animé d'un mouvement de la forme

F = F0 + F1 sin wt

    l'erreur e max apparaît pour les valeurs extrêmes de sin wt, soit pour

wt = ± 90°.

    Les valeurs des différents paramètres ou variables sont dans un premier temps les suivantes :

    Calcul de D

    D: valeur crête à crête du déplacement.

    D = XC1 - XC2

    XC2  = - Lsin(F0 + F1)

             = - L(sinF0cosF1 + sinF1cosF0)

                                                                              XC1 = -Lsin(F0 - F1)         

                                                                                      = - L(sinF0 cosF1 -sinF1cosF0)

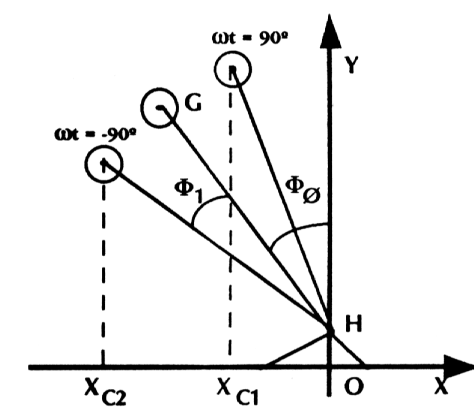Figure 2 : Schéma des notations conventionnelles utilisées pour le calcul de l'erreur relative.

3 ) Equations de départ

D = 2LsinF 1cosF 0 (1)

(2)

Sachant que 1-sin2 F = cos2 F , il vient:

F = F0 + F1 sin wt (3)

F ' = F1 w cos wt (4)

F " = - F1 w2 sin wt (5)

 

erelatif = er = e / D (6)

er % = 100 er (7)

4 ) Valeurs numériques particulières

L = 1 m

h = 0,10 m

g = 10 m/s2

t = ± 90°

sin wt = ± 1

cos wt = 0

F = F0 ± F1

F' = 0

F" = ± F1 w2

 

5) Equations utilisées

D = 2 sinF1cosF0                         (1)

                       (2)

F = F0 + F1 pour wt = + 90°       (3)

F = F0 - F1 pour wt = - 90°         (3')

F" = - F1 w2 pour wt = + 90°      (4)

F" = F1 w2 pour wt = - 90°         (4')

er = er = e / D                                 (5)

er % = 100 er                                 (6)

6 ) Résultats

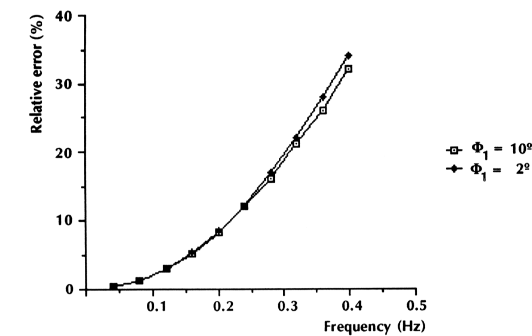Figure 3: Erreur relative en fonction des fréquences et de l'amplitude des oscillations. L'erreur relative dépend nettement de la fréquence, mais non de l'amplitude des oscillations étudiées (2° et 10°).

    Les résultats sont présentés sous forme de courbes à la figure 3. L'échelle des erreurs relatives est logarithmique. La courbe 'carrés blancs' : F= ± 10°, la courbe 'carrés noirs' : F= ± 2°. L'importance de l'erreur relative ne dépend pratiquement que de la fréquence.

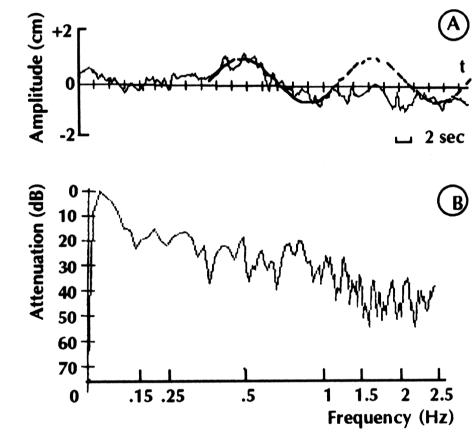Figure 4 : Stabilogramme droite-gauche (A) et transformée de Fourier (8) d'un sujet présentant une atténuation importante de ses oscillations en fonction des fréquences

    Si la fondamentale du signal est très basse (0,05 Hz sur la figure 4) et l'atténuation des oscillations importante en fonction des fréquences, on constate que le centre de pression est porté à ses positions extrêmes, qui déterminent la valeur de la surface du statokinésigramme, par une grande oscillation d'une période de 18 secondes (Figure 4) pour laquelle la position du centre de pression coincide avec la projection du centre de gravité à une erreur près de 0,4%. Les petites oscillations surajoutées, de l'ordre de 0,4 Hertz, mesurent les oscillations du centre de gravité à une erreur près qui est considérable, de l'ordre de 30% de crête à crête, soit 15% de l'amplitude qui intervient pour modifier la valeur de la surface, mais elles ne représentent que 10% de l'amplitude de la fondamentale, elles n'introduisent donc qu'une erreur de l'ordre de 1,5%. Ce qui est d'autant plus négligeable que l'algorithme de calcul de la surface élimine 10% des positions extrêmes du centre de pression.

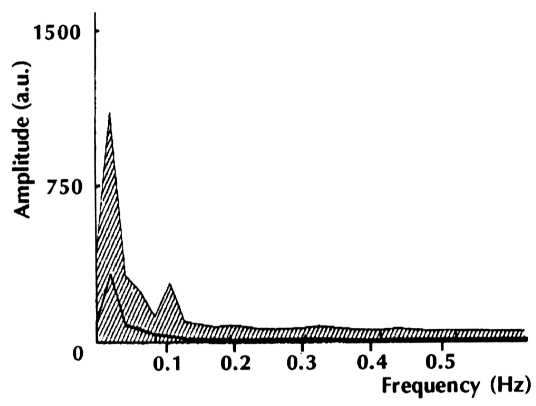Figure 5 : Moyenne et  Décile 90 du spectre d'amplitude des oscillations antéro-postérieures de 91 sujets normaux. (d'après Gagey, 1986)

    Les études statistiques sur le spectre d'amplitude des sujets normaux montrent que la fondamentale est à 0,04 Hz, que l'atténuation à 0,4 Hertz est largement supérieure à 10% (Figure 5) (Gagey, 1986).

    On peut donc considérer qu'on commet une erreur minime en assimilant les déplacements du centre de pression aux déplacements du centre de gravité pour mesurer la stabilité moyenne de l'homme normal, à condition que l'hypothèse du pendule inversé qui était à la base des calculs soit respectée.

Bibliographie

Bizzo G. (1993) Étude dynamique de la plate-forme. in Gagey P.M. (Eds) Huit Leçons de Posturologie.: 33-38. AFP (Paris).

Gurfinkel V.S. - Physical foundations of stabilography. Agressologie, 14, C, 9-14, 1973,a.