 |
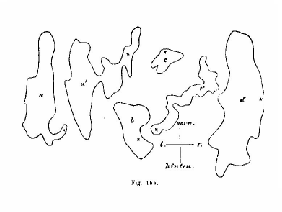
FIG. 1 - Oscillations posturales enregistrées par Vierordt vers 1860. |
Vierordt avait raison
Vierordt, dès le milieu du XIXe siècle, avait compris que le corps de l'homme n'est jamais en équilibre, toujours à la recherche de cet instant éphémère au cours duquel s'annulent toutes les forces en action sur sa masse corporelle (Vierordt, 1860). Et Vierordt a cherché à pénétrer cette dynamique fluctuante en enregistrant les oscillations posturales, sûr que ce petit gribouillis était très riche d'informations (fig. 1).
 |
FIG. 1 - Oscillations posturales enregistrées par Vierordt vers 1860. |
Effectivement depuis
une trentaine d'années l'analyse du signal stabilométrique
montre que Vierordt avait raison. Plus nous développons
nos analyses, conventionnelles, fréquentielles, stochastiques,
plus nous constatons que la foi de Vierordt était fondée.
Alors l'analyse dynamique
non-linéaire, pourquoi pas? D'ailleurs elle a déjà
donné quelques preuves d'une puissance assez exceptionnelle
(Gagey et al, 1998; Sasaki et al., à paraître).
Mais elle n'est pas évidente à comprendre, il faut
s'y préparer.
Comprendre Takens
À première
vue le signal stabilométrique n'est qu'un ensemble de points
dont on a relevé les coordonnées dans un référentiel
biomécanique...
Mais ces points sont ordonnés
dans le temps, et la logique de la stabilisation nous permet de
comprendre intuitivement que la position d'un point à l'instant
t dépend de la position du point à l'instant t-1:
le corps revient en arrière parce qu'il était allé
trop en avant, etc.
Autrement dit cette série temporelle
est récursive, ce qui se passe à l'instant t est
fonction de ce qui s'est passé à l'instant t-1:
|
|
Ces points nous «racontent
une histoire», pourrait-on dire de façon plus imagée;
en eux sont inscrits les fruits d'un mouvement, d'une dynamique...
Or ces points sont les points d'application
de la résultante des forces que la plate-forme oppose aux
forces exercées sur elle par le corps du sujet. L'histoire
que nous conte le signal stabilométrique est donc une histoire
de forces, c'est-à-dire de masses, d'accélérations,
de vitesses, une histoire de dynamique, une dynamique de dynamique
pourrait-on dire pour jouer sur les deux sens du terme.
Et ces dynamiques dépendent de facteurs
neurophysiologiques très nombreux, à commencer par
toutes les entrées du système postural fin: visuelle,
vestibulaire, extéroceptive plantaire, proprioceptive,
etc.
Ainsi dans cette série temporelle récursive,
la position de chaque point est déterminée par un
grand nombre de facteurs.
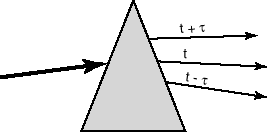
Malheureusement les rôles joués par chacun de ces facteurs sont intriqués, confondus, un peu comme sont confondues toutes les couleurs de l'arc-en-ciel dans la lumière blanche. Pour séparer les différentes couleurs contenues dans la lumière blanche il faut qu'elle soit diffractée à travers un prisme optique. De la même manière - si l'on peut dire - grâce au théorème de Takens, l'analyse dynamique non-linéaire diffracte l'effet des divers facteurs en passant le signal à travers un prisme temporel (fig. 2).
| FIG. 2 - Comparaison
du théorème de Takens à un prisme temporel. L'effet des divers facteurs est diffracté, sur un instant étendu de t - kt à t + kt. (k=1 sur la figure) |
 |
À chacun des n facteurs qui déterminent la position du centre de pression, on attribue -sans les désigner-:
Ces n coordonnées donnent la position du point-image du système à «l'instant t», dans cet espace mathématique à n dimensions, dit «espace des phases» (fig. 3).
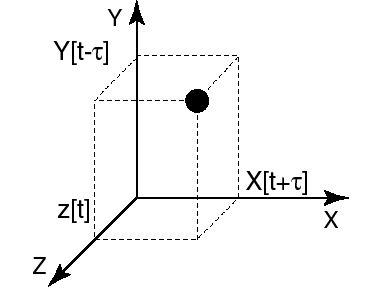 |
FIG. 3 - Construction d'une image
de la dynamique du système dans «l'espace des phases». +t pour le facteur X, -t pour le facteur Y, 0 pour le facteur Z. |
La trajectoire du point-image dans l'espace des phases (fig. 4) permet de suivre l'évolution des divers facteurs au cours du temps.
| FIG. 4 - Exemple de trajectoire dans l'espace des phases: l'attracteur de Lorentz. | 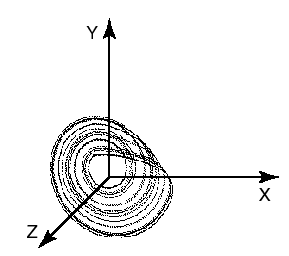 |
À quoi ça sert?
Cette image de la dynamique
du système dans l'espace des phases peut être exploitée
de diverses manières.
Comme les différents facteurs qui interviennent
dans la dynamique du système sont distingués dans
l'espace des phases, mais non nommés, il serait
certes possible mais totalement inutile de suivre l'évolution
de chaque facteur car d'une part on ne saurait pas de quoi il
s'agit -le facteur est innominé-, d'autre part cette évolution
ne serait autre que le signal stabilométrique lui-même!
La série des X[t+kt] est identique à la série des X[t],
à quelques termes extrêmes près.
Par contre il est possible de «compter»
ces facteurs (Grassberger & Procaccia, 1983; Sugihara &
May, 1990) pour répondre à une question importante:
Plus nombreux sont les facteurs
qui interviennent dans la dynamique d'un système, plus
nombreux sont ses degrés de liberté.
Il est possible aussi de comparer les images
de deux systèmes différents (Le Van Quyen et
al., 1999) pour évaluer:
Une application de l'analyse dynamique non-linéaire
L'analyse dynamique non-linéaire
s'est révélée nettement plus performante
que les analyses conventionnelles, fréquentielles et stochastiques
au cours d'une étude de l'adaptation du système
postural fin au port de verre prismatique (Gagey et al.,
1998).
Les analyses conventionnelles ne montraient
qu'une très discrète réaction du système
postural fin et uniquement pendant les premières
minutes de l'adaptation au port de verres correcteurs
prismés (fig. 5),
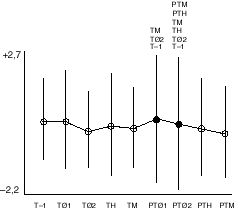 |
FIG. 5 - Adaptation
posturale au port de verres correcteurs. Moyennes et écart-types du paramètre VFY avant (temps T-1) et au cours de l'adaptation au port de verres correcteurs (temps PTx). La seule différence statistiquement significative porte sur la variance : À la troisième minute (PTØ1) et à la sixième minute (PTØ2) du port de verres prismés la variance de la distribution est significativement différente. Mais cette différence a complètement disparu après trois heures (PTH) et après trois semaines (PTM) de port des verres prismés. N=34, situation yeux ouverts (D'après Gagey et al., 1998). |
Alors qu'un
mois après le début de la phase d'adaptation
aux verres prismés, l'analyse dynamique non linéaire
mettait encore en évidence une réduction des degrés
de liberté du système (fig. 6).
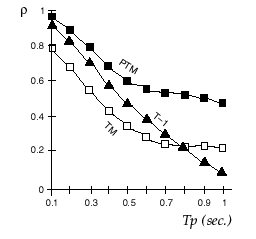 |
FIG. 6 - Adaptation
posturale au port de verres correcteurs. Coefficients de corrélation, r, entre les images du système, prédites et réelles, selon l'intervalle de prédiction, Tp, (algorithme de Sugihara-May), Avant l'expérience (T-1), après un mois de port de verres prismés (PTM) et non prismés (TM). Les résultats des temps intermédiaires (TØ, etc.) ont été supprimés du graphique pour plus de clarté. On constate une réduction des degrés de liberté du système postural fin qui persiste un mois après le début de l'adaptation aux verres prismés. Un sujet en situation yeux ouverts, (D'après Gagey et al., 1998). |
Conclusion
L'analyse dynamique
non-linéaire est encore du domaine de la recherche clinique:
On ne peut pas encore dire à quoi elle servira, ni même
si elle servira à quelque chose!...
Elle requiert une type spécial de plate-forme
capable d'échantillonner correctement le signal à
40 Hertz.
Bibliographie
Gagey P.M., Martinerie J., Pezard L., Benaim Ch. (1998)
L'équilibre statique est contrôlé par un système
dynamique non-linéaire. Ann. Oto-Laryngol., 115:
161-168.
Grassberger P., Procaccia I. (1983) Phys. Rev. Lett., 50,
346-369.
Le Van Quyen M., Martinerie J., Adam C., Varela F.J. (1999) Nonlinear
analyses of interictal EEG map the brain interdependences in human
focal epilepsy. Physica D, 127 : 250-266.
Sasaki O., Gagey P.M., Ouaknine M., Martinerie J., Le Van Quyen
M., Toupet M., L'Héritier A. Nonlinear Analysis of orthostatic
posture in vestibulopathy (article soumis)
Sugihara G., May R.M. (1990) Nonlinear forcasting as a way of
distinguishing chaos from measurement error in time series. Nature,
344: 734-741.
Vierordt Karl von (1860/ 1862/ 1864/ 1871/ 1877) Grundriss
der Physiologie des Menschen. H. Laupp, Tuebingen.